链表的总结

链表

链表（Linked list）是一种常见的基础数据结构，是一种线性表，但是并不会按线性的顺序存储数据，而是在每一个节点里存到下一个节点的指针(Pointer)。由于不必须按顺序存储，链表在插入的时候可以达到O(1)的复杂度，比另一种线性表顺序表快得多，但是查找一个节点或者访问特定编号的节点则需要O(n)的时间，而顺序表相应的时间复杂度分别是O(logn)和O(1)。 —wiki

单向链表

链表中最简单的一种是单向链表，它包含两个域，一个信息域和一个指针域。这个链接指向列表中的下一个节点，而最后一个节点则指向一个空值。

单向链表的基本操作

//基本结构
typedef int ElmeType;
typedef struct Lnode{
    ElemType val;
    struct Lnode *next;
}Lnode;

//构造线性表,头插法，将节点插入到表头，这样构成的线性表就是与输入的顺序相反
Lnode* addListH(Lnode *Lhead, int v)
{
    Lnode *newNode = (Lnode *)malloc(sizeof(Lnode));
    if (newNode == NULL){
        fprintf(stderr, "malloc failure\n");
        exit(EXIT_FAILURE);
    }
    newNode->val = v;
    newNode->next = NULL;
    
    newNode->next = Lhead;
    Lhead = newNode;
    
    return Lhead;
}
//尾插法
Lnode *addListR(Lnode *Lhead, Elemtype v)
{
    Lnode *newNode = (Lnode *)malloc(sizeof(Lnode));
    if (newNode == NULL){
        fprintf(stderr, "malloc failure\n");
        exit(EXIT_FAILURE);
    }
    newNode->val = v;
    newNode->next = NULL;
    
    Lnode *front = NULL, *rear = NULL;
    
    if (front == NULL)
        front = newNode;
    else
        rear->next = newNode;
    rear = newNode;
    return front;
}

//本算法取出单链表L（带头结点）中第i个位置的结点指针
LNode* GetElemAddr(Lnode* h, ElemType i){
    int j=1;  //计数，初始为1
    LNode *p = h;  //头结点指针赋给p
    if(i == 1)
        return L;  //若i等于1，则返回头结点
    if(i < 1)
        return NULL;  //若 i 无效，则返回 NULL
    while( p && j < i ) {  //从第1个结点开始找，查找第i个结点
        p=p->next;
        j++;
    }
    return p; //返回第i个结点的指针，如果i大于表长，p=NULL，直接返回p即可
}

//本算法查找单链表 L （带头结点）中数据域值等于e的结点指针，否则返回NULL
LNode *LocateElem (Lnode *h, ElemType e) {
    LNode *p= h;
    while( p != NULL && p->data !=e)  //从第1个结点开始查找data域为e的结点
        p=p->next;
    return p;  //找到后返回该结点指针，否则返回NULL
}

插入操作

在某个节点以后插入一个节点

//将s节点插入到第i个位置
Lnode* temp = GetElemAddr(h, i-1);
s->next = temp->next;
temp->next = s;

前插操作
扩展：对某一结点进行前插操作

前插操作是指在某结点的前面插入一个新结点，后插操作的定义刚好与之相反，在单链表插入算法中，通常都是釆用后插操作的。

以上面的算法为例，首先调用函数GetElem()找到第i-1个结点，即待插入结点的前驱结点后，再对其执行后插操作。由此可知，对结点的前插操作均可以转化为后插操作，前提是从单链表的头结点开始顺序查找到其前驱结点，时间复杂度为O(n)。

此外，可以釆用另一种方式将其转化为后插操作来实现，设待插入结点为s，将插入到p的前面。我们仍然将s插入到p的后面，然后将p->data与s->data交换即可，这样既满足了逻辑关系，又能使得时间复杂度为O(1)。算法的代码片段如下：

//将结点插入到*P之前的主要代码片段
s->next = p->next; //修改指针域，不能颠倒
p->next = s;
temp = p->data;  //交换数据域部分
p->data=s->data;
s->data=temp;

双向链表

wiki中实现的双向链表
此时，双向链表的头结点不放任何数据，只作索引作用(终止作用)，这时的双向链表是循环的，最后一个节点的next指针指向头结点，头结点的prev指针指向最后一个节点

循环链表

链表的相关面试题

Reverse Linked List

利用头插法翻转链表

class Solution {
public:
    ListNode* reverseList(ListNode* head) {
        ListNode* newHead = NULL;    
        ListNode* temp =NULL;       //存储当前要反转的节点
        while(head != NULL){
            temp = head;
            head = head->next
            
            //尾插法
            temp->next = newHead;
            newHead = temp;
            
        }
        return newHead;
    }
};

Reverse Linked List II

反转特定区间的节点
解体思路:记住开始反转的节点start, 它的前一个节点prev, 则就转为将prev->start->temp(start->next)变成prev->temp->start，即将start的后一个节点循环加入到start的前面，插入后start指向它的下下一个节点。

class Solution {
public:
    ListNode* reverseBetween(ListNode* head, int m, int n) {
        
        ListNode *start = NULL, *temp = NULL;   
        ListNode dummy(0);
        dummy.next = head;
        
        ListNode *prev = &dummy;
        
        if (head == NULL || head->next== NULL || m == n)
            return head;
            
        int i = 1;        
        for( ;i <  m; i++)
            prev = prev->next;
        
        start = prev->next;
        
        for(; m < n; m++){
            temp = start->next;
            
            start->next = temp->next;
            temp->next = prev->next;
            prev->next = temp;
        }
        
        return dummy.next;
    }
};

Rotate List

解体思路：题目是将右移，可以把它变成循环链表，移完后再记录下当前的头结点和尾节点，再拆分,此处需要注意的是当k大于链表的长度的时候，相当于对链表长度的余数

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    ListNode* rotateRight(ListNode* head, int k) {
        if (head == NULL  || head->next == NULL || k == 0)
            return head;
        
        ListNode *prev = head;
        int len = 1;
        //prev指向尾节点
        while(prev->next != NULL){
            prev = prev->next;
            len++;
        }
            
        k = len - k % len;
        prev->next = head;     //首尾相连
        
        while(k > 0){
            prev = prev->next;
            k--;
        }
        head = prev->next;
        prev->next = NULL;
        return head;
    }
};

解法一：新构造一个链表，复制原有链表的label，但是在给新的链表的随机指针(random)赋值时，每次都需要重新遍历一遍原有的链表，来确定随机指针指向的节点(或NULL)，可以使用hash表来解决上述查询问题，建立原有节点到现节点的map，这样在查找新链表的随机指针时，找到原有节点的随机指针的指向，在根据这个地址来寻找它在新链表的位置,
这会额外使用O(n)的map空间
第一步：使用HashMap，首先复制所有的节点，用HashMap记录老节点A与新节点A’的映射关系。

第二步：遍历每个点，将Random指针连上。如存在一条Random指针从A指向B，那么在HashMap中找到映射的新节点A’和B’，将A’的Random指针指向B’。

/**
 * Definition for singly-linked list with a random pointer.
 * struct RandomListNode {
 *     int label;
 *     RandomListNode *next, *random;
 *     RandomListNode(int x) : label(x), next(NULL), random(NULL) {}
 * };
 */
class Solution {
public:
    RandomListNode *copyRandomList(RandomListNode *head) {
        if (head == NULL) return NULL;
        
        map<RandomListNode *, RandomListNode *> ma;
        RandomListNode *newHead = new RandomListNode(head->label);
        ma.insert(make_pair(head, newHead));
        RandomListNode *p = head->next;
        RandomListNode *q = newHead;
        //构造新链表
        while(p){
            //产生新节点，插入到新链表中
            RandomListNode *temp = new RandomListNode(p->label);
            q->next = temp;
            
            ma.insert(make_pair(p, temp));
            
            p = p->next;
            q = q->next;
        }
        
        //拷贝随机指针
        p = head;
        q = newHead;
        while(p){
            q->random = ma[p->random];
            p = p->next;
            q = q->next;
        }
        
        return newHead;
    }
};

解法二：(1)将每个节点的复制节点插入到它的后面
(2)更新新插入节点的随机指针
(3)分离两个链表

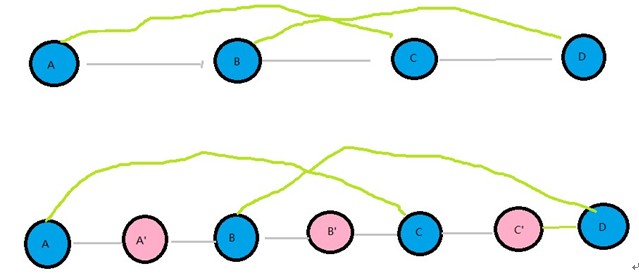
第一步：将每个节点复制并插入相邻节点中。如1->2->3->NULL变为：1->1’->2->2’->3->3’->NULL。

第二步：接下来连接Random指针，如果存在一条Random指针从A指向B，那么将A->next的Random指针指向B->next。

第三步：将链表拆开。A=head, A’=head->next; A->next=A->next->next；A’->next=A’->next->next; …

/**
 * Definition for singly-linked list with a random pointer.
 * struct RandomListNode {
 *     int label;
 *     RandomListNode *next, *random;
 *     RandomListNode(int x) : label(x), next(NULL), random(NULL) {}
 * };
 */
class Solution {
public:
    RandomListNode *copyRandomList(RandomListNode *head) {
        
        if (head == NULL) return NULL;
        
        RandomListNode *p = head;
        //构造成a->a'->b->b'->c->c'.....
        while(p){
            RandomListNode *temp = new RandomListNode(p->label);
            temp->next = p->next;
            p->next = temp;
            
            p = p->next->next;
        }
        
        p = head;
        //更新随机指针
        while(p){
            if (p->random)
                p->next->random = p->random->next;
                
            p = p->next->next;
        }
        
       /* //分离链表
        p = head;
        RandomListNode *newHead = p->next;
        while(p){
            RandomListNode *q = p->next;
            RandomListNode *temp = p->next->next;
            if(temp == NULL){     //此时到达最后一个节点temp == NULL
                p->next = NULL;
                q->next = NULL;
            }else{
                q->next = temp->next;
                p->next = temp;
            }
            
            p= p->next;
            
        }*/
        
        //分离链表
        p = head;
        RandomListNode *newHead = p->next;
        while(p){
            RandomListNode *q = p->next;
            p->next = q->next;
            
            //考虑这种情况d -> d'-> NULL,是否到达末端
            if (q->next)    
                q->next = q->next->next;
            
            p= p->next;
        }
        return newHead;
    }
};

Sort List

解体思路:首先题目规定的时间为$O(n \log n)$,那么首先想到的就是归并排序了
(1)要归并，首先得求链表的中点，在中点处将链表断开
(2)合并两个已经排好序的链表
求链表的中点

/*
 *一种不好的求中点的方法,这种方法的缺点在于当只有两个节点的时候，例如a->b,
 *返回的是a->b, NULL的划分(这个会对以后的合并造成很大的影响)，而需要的则是
 *a，b的划分
 */
ListNode *getMiddle(ListNode *h)
{
    if (head == NULL && head->next == NULL)
        return head;
        
    ListNode *fast, *slow;
    slow = fast = head;
    
    while(fast && fast->next){
        slow = slow->next;
        fast = fast->next->next;
    }
    
    return slow;
}

完整代码

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    ListNode* sortList(ListNode* head) {
        if(!head || !head->next)
            return head;
        
        //找到中间节点
        ListNode dummy(-1);
        dummy.next = head;
        
        ListNode *slow, *fast;
        slow = fast = &dummy;
        
        while(fast && fast->next){
            slow = slow->next;
            fast = fast->next->next;
        }
        
        //从中间分开
        ListNode *middle = slow->next;
        slow->next = nullptr;
        
        ListNode *h1 = sortList(head);
        ListNode *h2 = sortList(middle);
        
        return merge(h1, h2);
    }
private:
    ListNode *merge(ListNode *l1, ListNode *l2){
        ListNode dummy(-1);
        ListNode *p = &dummy;
        while(l1 && l2){
            if(l1->val <= l2->val){
                p->next = l1;
                l1= l1->next;
            }else{
                p->next = l2;
                l2 = l2->next;
            }
            p = p->next;
        }
        if(l1 == nullptr) p->next = l2;
        else p->next = l1;
        
        return dummy.next;
    }
}；

链表总结

链表