求出两个排好序的数组的中位数

Median of Two Sorted Arrays

There are two sorted arrays nums1 and nums2 of size m and n respectively. Find the median of the two sorted arrays. The overall run time complexity should be O(log (m+n)).
link
题目大意，给定两个排好序的数组，求出中位数，这里需要注意的是，当两个数组的长度之和为偶数时，有两个中位数。

merge的方法

解法一:照着mergeSort中merge的方法，合并到中位所在的位置。算法复杂度为O(m+n)

class Solution {
public:
    double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) {
        int len1 = nums1.size();
        int len2 = nums2.size();
        
        int len = len1 + len2;
        //i遍历nums1, j遍历nums2
        int i = 0, j = 0;
        //cur记录合并两数组到达的数，prev是它的前一个数
        int prev = 0, cur = 0;
        while((i+j) <= len/2){
            prev = cur;
            if(i >= len1)
                cur = nums2[j++];
            else if(j >= len2)
                cur = nums1[i++];
            else if(nums1[i] < nums2[j])
                cur = nums1[i++];
            else 
                cur = nums2[j++];
        }
        if(len & 1)
            return cur;
        else
            return (prev + cur)/2.0;
    }
};

二分的方法

参阅:
http://fisherlei.blogspot.com/2012/12/leetcode-median-of-two-sorted-arrays.html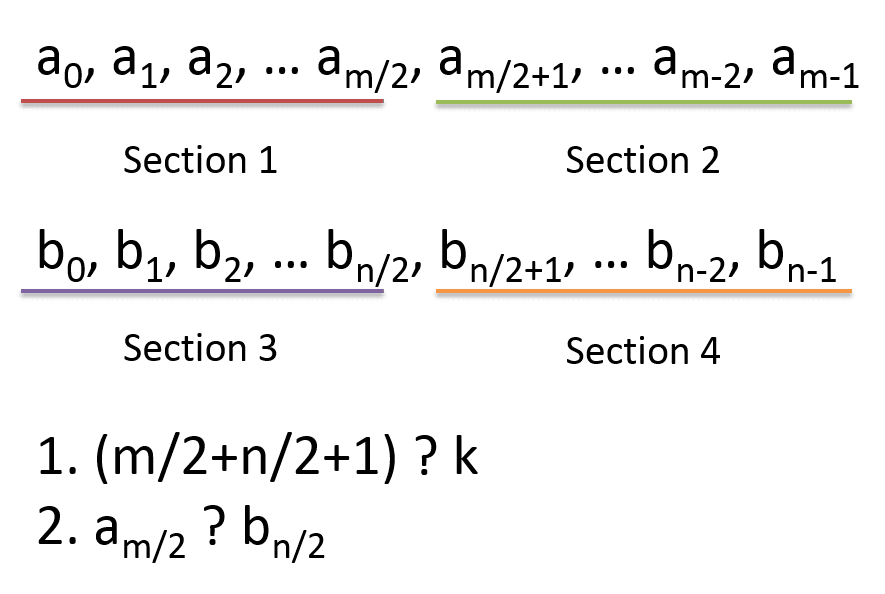

这篇文章主要是每次取出各自数组的一半(只跟数组的长度有关)，
如果 (m/2 + n/2) > k，那么意味着，当前中位数取高了，正确的中位数要么在 Section 1或者Section3中。如果A[m/2] > B[n/2], 意味着中位数肯定不可能在Section 2里面，那么新的搜索可以丢弃这个区间段了。同理可以推断出余下三种情况，如下所示：

If (m/2+n/2+1) > k && am/2 > bn/2 , drop Section 2
If (m/2+n/2+1) > k && am/2 < bn/2 , drop Section 4
If (m/2+n/2+1) < k && am/2 > bn/2 , drop Section 3
If (m/2+n/2+1) < k && am/2 < bn/2 , drop Section 1
http://www.acmerblog.com/leetcode-median-of-two-sorted-arrays-5330.html
这篇文章的方法较好，也是最后确定的方法。

解法:对于一个长度为n的已排序数列a，若n为奇数，中位数为a[n / 2 + 1] , 若n为偶数，则中位数(a[n / 2] + a[n / 2 + 1]) / 2,如果我们可以在两个数列中求出第K小的元素，便可以解决该问题
不妨设数列A元素个数为n，数列B元素个数为m，各自升序排序，求第k小元素
取A[k / 2] B[k / 2] 比较，
如果 A[k / 2] > B[k / 2] 那么，所求的元素必然不在B的前k / 2个元素中(证明反证法)
反之，必然不在A的前k/2个元素中，于是我们可以将A或B数列的前k / 2元素删去，求剩下两个数列的k - k / 2小元素，于是得到了数据规模变小的同类问题，递归解决
如果 k / 2 大于某数列个数，所求元素必然不在另一数列的前k / 2个元素中，同上操作就好。

class Solution {
public:
    double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) {
        //int len1 = nums1.size();
        //int len2 = nums2.size();
        int len = nums1.size() + nums2.size();
        
        if( len % 2 != 0)
            return findKth(nums1, 0, nums2, 0, len/2 + 1);
        else
            return ( findKth(nums1, 0, nums2, 0, len/2) + findKth(nums1, 0, nums2, 0, len/2 +1) )/2.0;
    }
private:
    //从两个数组中找到第k个元素
    int findKth(vector<int> & nums1, int start1, vector<int> &nums2, int start2, int k){
        if(start1 >= nums1.size())
            return nums2[start2 + k-1];
        if(start2 >= nums2.size())
            return nums1[start1 + k -1];
        if (k == 1)
			return min(nums1[start1], nums2[start2]);
        int key1 = start1 + k/2  -1 < nums1.size() 
                   ? nums1[start1 + k/2 -1]
                   : INT_MAX;
        int key2 = start2 + k/2 - 1 < nums2.size() 
                   ? nums2[start2 + k/2 -1]
                   : INT_MAX;
        
        if(key1 < key2)
            return findKth(nums1, start1 + k/2, nums2, start2, k - k/2);
        else
            return findKth(nums1, start1, nums2, start2 + k/2, k - k/2);
    }
};

上面需要方法可能发生某个数组的长度偏小，造成数组索引超出范围，上面采用的方法是，当数组索引超出时，取整数的最大值，从而保留了整个数组，
下面的方法是采用求出k/2与数组长度len的最小值，从而确定出比较的范围，避免了采用INT_MAX

int findKth(int *arr1, int len1, int *arr2, int len2, int k){
    //assume len1 < len2
    if(len1 > len2)
        return findKth(arr2, len2, arr1, len1, k);
        
    if(len1 == 0)
        return arr2[k-1];
    
    if( k == 1)
        return arr1[0]< arr2[0]?arr1[0]:arr2[0];
    //两个数组的各自的分割点pivot    
    int split = len1 < k/2 ? len1:k/2;
    
    if(arr1[split - 1] < arr2[split - 1])
        return findKth(arr1 + split, len1 - split, arr2, len2, k - split);
    else
        return findKth(arr1, len1, arr2 + split, len2 - split, k - split);
}

double findMedianSortedArrays(int* nums1, int nums1Size, int* nums2, int nums2Size) {
    int len = nums1Size + nums2Size;
        
    if(len & 1)
        return findKth(nums1, nums1Size, nums2, nums2Size, len/2 + 1);
    else
        return (findKth(nums1, nums1Size, nums2, nums2Size, len/2) + findKth(nums1, nums1Size, nums2, nums2Size, len/2 + 1) )/2.0;
}

更新:上面的方法每次只能剔除split以前的元素，即split个元素，下面采用的方法是每次从两个数组的数字之和为k个元素，比如说arr1,取出split1个元素，arr2取出k-split1个元素。这种方法中，少了k==1会导致[1][1]这种测试用runtime error。仔细想了想，当为[1][1]时，len = 2,意味着要返回k=2和k=1这两种情况。k=2时split1 = 1, split2 = 1，能正常工作;k=1时，split1 = 0， split2 = 1，先然后面要调用split -1会造成非法访问

int findKth(int *arr1, int len1, int *arr2, int len2, int k){
    //assume len1 < len2
    if(len1 > len2)
        return findKth(arr2, len2, arr1, len1, k);
        
    if(len1 == 0)
        return arr2[k-1];
    
    if( k == 1)
        return arr1[0]< arr2[0]?arr1[0]:arr2[0];
    //两个数组的各自的分割点pivot    
    int split1 = len1 < k/2 ? len1:k/2;
    int split2 = k - split1;
    //此处给出了split1 - 1的算式，也就意味着split>=1，即默认k>=2,k==1的情况要单独判断
    if(arr1[split1 - 1] < arr2[split2 - 1])
        return findKth(arr1 + split1, len1 - split1, arr2, len2, k - split1);
    else if(arr1[split1 - 1] > arr2[split2 - 1])
        return findKth(arr1, len1, arr2 + split2, len2 - split2, k - split2);
    else
        return arr1[split1 -1];
}

double findMedianSortedArrays(int* nums1, int nums1Size, int* nums2, int nums2Size) {
    int len = nums1Size + nums2Size;
        
    if(len & 1)
        return findKth(nums1, nums1Size, nums2, nums2Size, len/2 + 1);
    else
        return (findKth(nums1, nums1Size, nums2, nums2Size, len/2) + findKth(nums1, nums1Size, nums2, nums2Size, len/2 + 1) )/2.0;
}